[書式] FLOOR(<数値>,<基準値>)
[機能] <数値> を <基準値> の倍数に切り捨てます。
| <数値> | 切り捨てをおこないたい数値を指定します。 |
| <基準値> | 倍数の基準となる数値を指定します。 |
●●● 時間を10分ごとに切り捨てる方法 ●●●
今回は、時間の切り捨てについて考えていきましょう。
普通の数値の切り捨てなら ROUNDDOWN関数ですが、時間の場合には、そうはいきませ
ん。 たとえば1時間単位で切り捨てたいなら、1時間のシリアル値である 1/24 、すなわち
0.041666667 の倍数に切り捨てる必要があります。
さて、Excelには、FLOOR関数という、数値を任意の数値の倍数に切り捨てる関数があり
ます。 たとえば値を 0.25 ごとに切り捨てたければ、
=FLOOR(<数値>,0.25)
のように利用します。
こうすれば、<数値> が
「1.3」 だったら、計算結果は 「1.25」
「0.7」 だったら、計算結果は 「0.5」
というように、0.25の倍数に切り捨てることができます。
この関数をうまく利用すれば、時間の切り捨てもできそうですね。
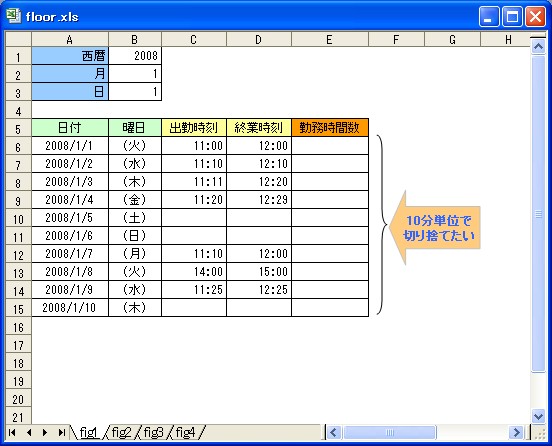
それでは例題として、これまで何度か出てきた次のシートを使って、「勤務時間数」を10分単位
で切り捨てる方法を考えていきましょう。
10分単位で切り捨てたいので、まず 「10分」 がシリアル値でいくつになるかを求めなければ
なりません。 時分秒からシリアル値を求めるには、TIME関数が便利でしたね。 この関数
を使って10分をシリアル値に変換するには、
=TIME(0,10,0)
という計算式が考えられます。
これを FLOOR関数に利用して、
=FLOOR(<切り捨てたい時間>,TIME(0,10,0))
とすれば、10分ごとの切り捨てができると考えられます。
ところで、Excelには、
「時間をあらわす文字列は、適宜、内部で時間のシリアル値に自動変換される」
という仕組みが備わっています。
そこで、同じことを
=FLOOR(<切り捨てたい時間>,"0:10:0")
という計算式でおこなうこともできます。
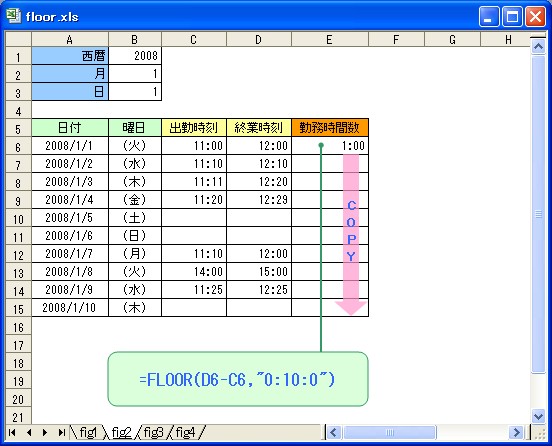
ということで、さっそく次の計算式を セルE6 に入力し、セルE15 までコピーしてみましょう。
=FLOOR(D6-C6,"0:10:0")
●●● 正しく計算されないのは??? 桁落ち ●●●
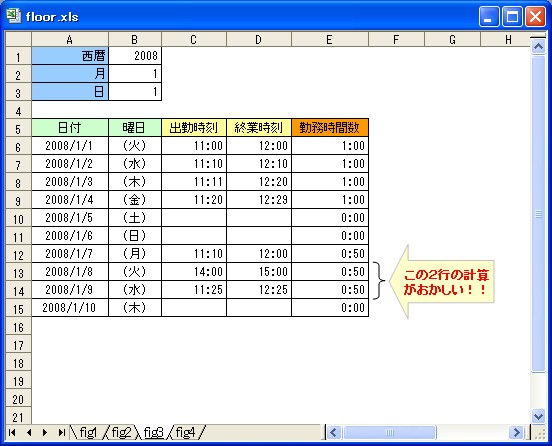
すると、次図のような結果になります。
一見、計算できたように思えますが、よくみると、正しない部分があります。
本来なら 「1:00」 という結果になるところが 「0:50」 となっています。
考え方は正しいはずなのに、正しく計算されないのです。
これは、「桁落ち」という、コンピュータ特有の現象によるものです。
ご存じのように、コンピュータの内部での計算は、二進数でおこなわれます。 このことは、
整数を扱う場合には特に問題になりません。
ところが、小数はどうでしょうか。 小数を二進数に直すと、多くの数でいつまでも続く無限
小数にります。 そして演算が行われる際に、有効数字が減少して誤差が生じることがあ
るのです。 これを 「桁落ち」 と呼んでいます。
この時間の切り捨てでの計算誤差は、この桁落ちによるものと思われます。 つまり、
「 "15:00" から "14:00" を引いたら、桁落ちによって "1:00" にわずかばかり足りなくなった。
それをFLOOR関数で10分単位で切り捨てたので、50分という計算結果になってしまった」
と考えられるわけです。
●●● 時間の切り捨てを正しく計算するには ●●●
コンピュータの性質上やむを得ない現象ですが、でもだからといって、こんな計算違いが起こる
まま使うわけにはいきません。 では、どうしたらいいか。
時間の計算を自力でおこなう。 つまり、TEXT関数で文字列に変換して、コロンで分割して
60で掛けたり、割ったり、剰余を求めたり、なんていう方法もありますが、ちょっと面倒です。
ということで、
「足りないんなら、1秒足しちゃいましょう!」
なんていうおおざっぱなテクニックを考えるわけです。 このケースでは、計算は分までで、
秒は問題にしていません。そこで、たとえ1秒足したとしても、その後に FLOOR関数で
切り捨ててしまうので、問題は出ないと考えられます。
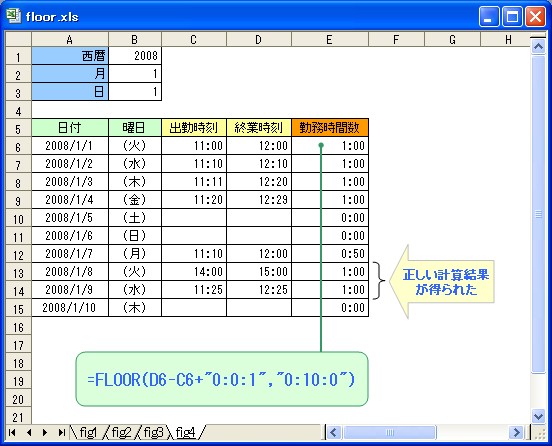
そこで今度は、セルE6の計算式を次のように変更して、セルE15までコピーしてみましょう。
=FLOOR(D6-C6-"0:0:1","0:10:0")
すると、今度は正しい計算結果が得られたはずです。
このように、小数の計算には意外な落とし穴がひそんでいます。 状況に応じて、きちんと
桁落ちの現象に対応することも、時には必要です。
「精密な計算をするわけではないから、桁落ちなんて関係ない」
と決めつけるのは早計です。 時間の計算も、Excelの内部では精密な小数の計算なの
ですから。